NFA vs DFA - Building a Regex Engine Part 10

At the beginning of this series I explained how regex engines were implemented with state machines, briefly mentioned the two main types (DFA and NFA) and jumped to NFA as fast as Sonic but without the Fortnite dance. Now it's time to explain in detail what are their differences and what would have changed if I had decided to use a DFA.

Put on your seatbelt because this post is going to be really long and probably useless.

NFA and DFA - The theory

Let's forget for a while about regex and just talk of finite automata as defined in formal language theory. A machine is formed by:

• A set of states $Q =\{q_0, q_1, q_2...\}$
• A number of transitions, often represented by a function with the form $\delta(<State>, <Input>) = <NextState>$
• A finite set of input symbols, called the alphabet ($\Sigma$)
• A starting state $q_0$, where $q_0$ is in $Q$ ($q_0$ $\in$ $Q$)
• A set of final states $F=\{q_x, q_y...\}$. It has to be a subset of $Q$ ($F\subseteq Q$)

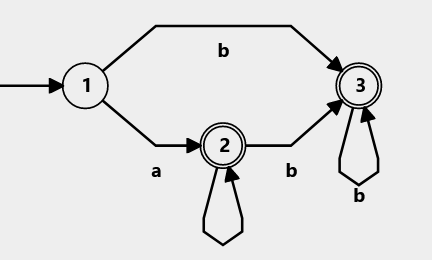
The transitions of the machine define whether it's deterministic (DFA) or non deterministic (NFA). A deterministic machine defines every single possible transition for every single state, but a state can't have two transitions that consume the same input. This way the machine just follows orders. It receives some input and just follows the corresponding transition. It doesn't have a choice.

Of course a lot of times there are transitions that aren't valid, and these are often represented as a transition going to a dead state. This is so common that most of the time they are implicit transitions, and they are ignored in diagrams. If a DFA doesn't have a transition, you can assume it goes to a dead state.

For example, here's a random machine for an alphabet $\Sigma=\{0,1,2\}$:

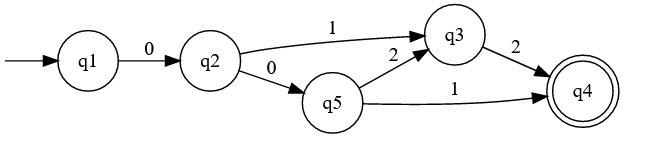
On the other hand, non-deterministic machines allows states to have two or more transitions that consume the same input. But then the machine needs to decide which transition to follow.

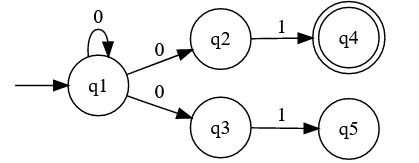
Even though it's a non deterministic machine, it still needs to return a deterministic result. So as long as one of the choices leads to a successfull state, then the machine succeeds. Therefore it needs some kind of mechanism to try all the options till either one succeeds or all fail. This could be backtracking or creating submachines that run in parallel.

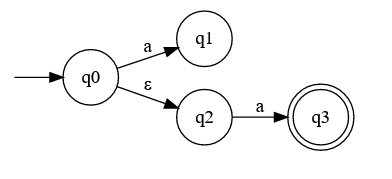
NFAs also allow epsilon transitions (transitions that don't consume input). I'm a bit confused about why DFA can't have them since I haven't seen it explicitly forbidden in its definition. The most logical argument I've seen is that that it could lead to machines that break the definition of DFA:

Practical differences between NFA and DFA

After all that theory you might be thinking: Who cares about the transitions a state has? Does it even matter? Do NFA have more recognizing power than DFAs?

NFAs and DFAs are equivalent. For every language recognized by a NFA you can find a DFA that also recognizes it. But that doesn't mean the difference between both doesn't matter. It all comes to the classic problem: Speed vs Memory ™.

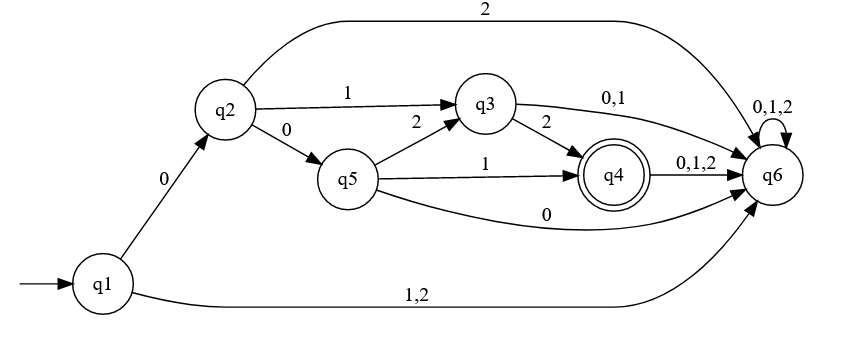
DFA are really fast because they don't have to make any decisions nor backtrack. They are just a lookup table. But since you can't have duplicated transitions, it can lead to a machine with MANY more states. If you transform a NFA with $n$ states to a DFA with the Powerset construction, the DFA can have up to $2^n$ states.

The worst case example can clearly be seen here:

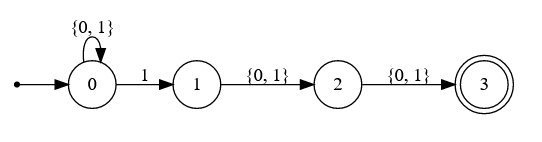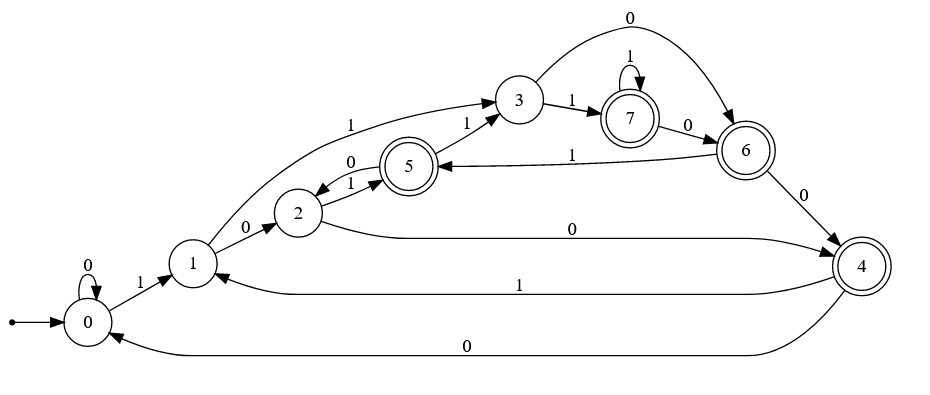NFA	DFA

I'm cherry picking a worst case scenario and most transformations aren't that bad. If you are curious about this specific case, it's explained really well in the post "Determinism costs! A NFA with exponentially bigger DFA" by Owen Stephens.

It's also important to highlight that there are DFA minimization algorithms (though the DFA above is already minimized) and there are not algorithms for NFA minimization. This is a PSPACE-complete problem (and maybe NP-hard? i'm confused). So in some cases a minimized DFA can have less states than a NFA.

In terms of time complexity, a DFA can compute a match in linear time. In the case of NFA, it depends on the algorithm. I haven't made the calculations of the backtracking approach, but Russ Cox says in his post "Regular Expression Matching Can Be Simple And Fast (but is slow in Java, Perl, PHP, Python, Ruby, ...)" that backtracking is $O(2^n)$ and the submachine implementation is $O(n^2)$.

For the people that don't like confrontation, there's a hybrid approach that also keeps the linear time at the cost of backreferences and lookarounds:

1. We implement an online DFA. That is, the DFA is constructed from the NFA during a search. When a new state is computed, it is stored in a cache so that it may be reused. An important consequence of this implementation is that states that are never reached for a particular input are never computed. (This is impossible in an "offline" DFA which needs to compute all possible states up front.)

2. If the cache gets too big, we wipe it and continue matching.

-- dfa.rs file in Rust's regex implementation https://docs.rs/regex/1.1.9/src/regex/dfa.rs.html

Rust's hybrid implementation is also $O(n)$. This section really makes my engine look bad, at least I should have made the submachine implementation 😅.

There are also some minor quetions that I find interesting (and don't know how to answer)

• Can NFAs be faster than DFAs if the DFA is significantly bigger?
• Do regex that suffer from catastrophic backtracking in NFAs lead to a DFA with a huge number of states? I tested the regex (x+x+)+y and the DFA is small. So does it affect the contruction time of the DFA in any way, or are DFAs completely inmune to stupid regex catastrophic backtracking?

NFA and DFA in modern regex engines

At this point we have already established that DFA's are the clear winner. NFAs are probably crying in a corner right now, right? Wrong. It's important to clarify that until know we were talking about the formal definition of NFA and DFA. So yes, if you just need a formal regex engine, go for DFA without a thought (unless you are low on RAM), but if you want the features of modern regex... things get complicated.

When talking about modern regex, NFAs have an incredible advantage: They are versatile, powerful and way WAY more intutive and explicit. NFA regex engines are often called "regex directed" while DFA are "text driven", and there's a reason: NFA machines resemble the pattern of the regex they recognize, so when it's executed it's almost as if the machine was following it. Meanwhile, in DFAs the states are more scrambled because it's compressing the alternatives to try all possibilities at the same time.

Let's see it with an example:

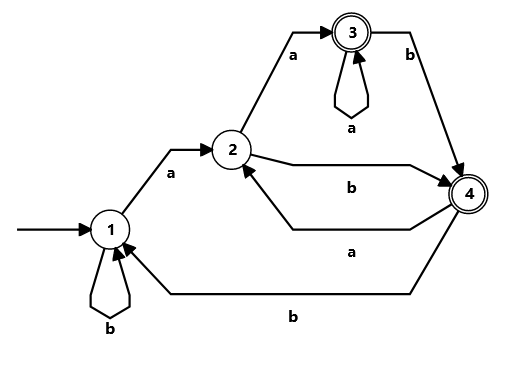
The fact that the NFA explicitly represents the pattern makes adding features much easier. And we have already seen this all over this series. Want to add capturing groups? Okay, just mark the states that start and end the group and check if you are on those. Want backreferences? Sure, add a transition that access memory and consumes a variable number of input.

Also, if the machine doesn't work just draw the diagram and see what's wrong. If you made a regex engine with the DFA regex above, and it failed, how long would it take you to find the bug?

I already made the NFA engine, so now it's time to recapitulate previous posts and think about what would have changed if I decided to make this a NFA engine.

The first post was just the introduction, and the second one was implementing a NFA. Programming a DFA would be even easier, in fact we could already use the NFA class to execute DFA (though that would be inneficient). A better implementation would be just like the NFA but without the backtracking algorithm.

The next post was about translating a formal regex to NFA. There are two ways to build a DFA from a regex:

1. Create a NFA using Thompson's constructions and then convert it to DFA with the Powerset construction.
2. Convert it directly to DFA

The problem is we need to modify the algorithms to implement modern features. And for me, the direct method doesn't seem too expandable, since it relies on calculating set of symbols. Were would we add the capturing groups? And the character classes complicate this a lot. So I'll assume we first calculate a NFA just like the ones I've talked through all these series.

But even with this method, the second post already presents a major problem: Lazyness.

Lazy quantifiers

DFA are always greedy. The end.

Okay, okay, I'll add some context. By default regex's quantifiers (+, *, ?) are greedy, which means they capture as many text as they can. But NFA-based engines have lazy versions of this quantifiers (+?, *, ?) which match the least text possible, even no text if they can.

In NFAs these quantifiers are implemented with loops like this one:

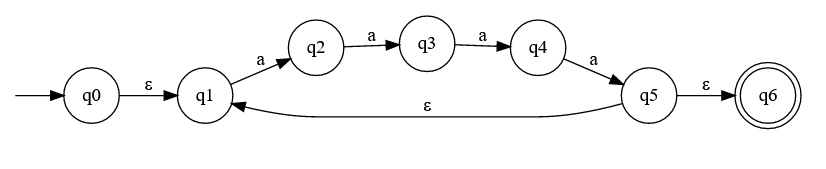
Here the state $q_5$ has two outward transitions: One that goes to $q_1$, continuing the loop, and another to $q_6$ that exits it. The NFA implements greediness and lazyness by prioritizing one transition over the other. And just at a concept level this is already incompatible with DFA. DFA just follow orders based on the input received. They can't choose whether to stay or exit.

Let's try to imagine how it could be done, beginning with a simple DFA for the regex a+:

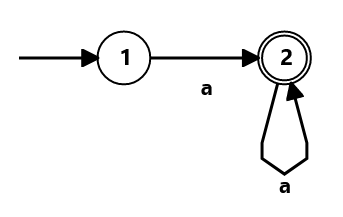
Now, how can this be done lazily? This just keeps consuming a as long as it can. You could make the DFA end as soon as it reaches the final state, which would work for this case but wouldn't when the loop isn't in the final state, like in a+b.

Let's try to image a DFA for a+?a. Here the lazyness is clear, because for the input aaaaaaaa it would only match aa. You might be tempted to implement another transition, like:

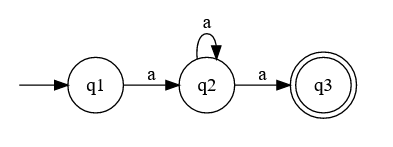
But that's already a NFA.

The root of the problem is that lazyness inherently implies backtracking, because you never now what's the least amount of input you can consume, so you try to consume an a, and see if that leads to a valid result. If it doesn't, consume another one and check again. Been greedy is easier: Just keep consuming a until it receives any other character.

Capturing groups in DFA

Implementing capturing groups in NFA was easy, since it's clear were a group starts and ends. The machine just needs to keep track of when it transverses a state that starts or ends a group. But with DFA... it's not that easy.

For the regex (a|b)*a(a|b):

In DFAs there's no clear states or transitions that start or end groups. So is it even possible? Yes, with TDFAs. But take this section with a grain of salt, since I investigated just enough to look as if I know how it works to make a broad exploanation.

TDFA (Tagged Deterministic Finite Automata) is an extension of DFA that allow submatch extraction (the fancy name for capturing groups). They do this by adding tags at cetain points of the regex, and the TDFA keeps track of the position when the tag is transversed. For example we can tag $(a)*(a|b)b*$ with five tags, represented with numbers $(1a2)*3(a|4b)5b*$ (I have no idea why this example has the tag 4, since it seems redundant with 3). This tags aren't literal characters, so you won't find a transition that consumes the number 1.

Each tag has a registry, that stores a position in the input string. Then each transition can define operations for those registries. There are two types (maybe?): n sets it to undefined and p sets it to the current position of the engine at that moment.

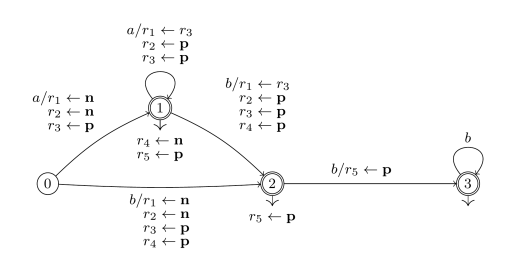
For example, to match string $aab$, one starts in state 0, matches the first $a$ and moves to state 1 (setting registers $r*{1}$ , $r*{2}$ to undefined and $r_{3}$ to the current position 0), matches the second $a$ and loops to state 1 (register values are now $r_{1}=0,r_{2}=r_{3}=1$, matches $b$ and moves to state 2 (register values are now $r_{1}=1,r_{2}=r_{3}=r_{4}=2$, executes the final operations in state 2 (register values are now $r_{1}=1,r_{2}=r_{3}=r_{4}=2,r_{5}=3$ and finally exits TDFA.

-- Wikipedia

This TDFA is not as optimial as the minimized DFA, but it still holds the other benefits of DFA

Canonical DFA solve the recognition problem in linear time. The same holds for TDFA, since the number of registers and register operations is fixed and depends only on the regular expression, but not on the length of input. The overhead on submatch extraction depends on tag density in a regular expression and nondeterminism degree of each tag (the maximum number of registers needed to track all possible values of the tag in a single TDFA state).

On one extreme, if there are no tags, a TDFA is identical to a canonical DFA. On the other extreme, if every subexpression is tagged, a TDFA effectively performs full parsing and has many operations on every transition. In practice for real-world regular expressions with a few submatch groups the overhead is negligible compared to matching with canonical DFA

-- Wikipedia (I'm too lazy to read the papers)

I'm sure there are other ways of handling submatch extraction, but TDFAs is the only one (I've seen) that is backed up by papers. I also read the post "A DFA for submatches extraction" by Nitely, which describes nDFA, but I wasn't really able to understand it (though I didn't try much). He didn't put any example, but he mentions that the DFA can be minimized. I wonder if it can be fully minimized (unlike TDFAs) and if the overhead of the prefix tree (both in memory and in query time) makes it better than TDFA. I have no idea, but the TDFA papers give me more trust than nDFA.

The classical conversion (from NFA to DFA) removes all the ε-transitions such as submatches, empty matches/zero-match assertions, repetitions, and alternations. However, we can keep a set/subset of the NFA transitions, and use them to contruct the submatches prefix-tree while executing the DFA.

-- A DFA for submatches extraction - Nitely (parenthesis added by me for context)

Character classes

In the fourth post I covered Character Classes, like [0-9] or \d to match any digit. These allow regex to be much more expressive because otherwise the same class would be written as (0|1|2|3||4|5|6|7|8|9). The implementation in NFA is simple, just add transitions that can match a set of characters. But formal regex don't have them, which is a problem because Powerset construction assumes all transitions consume single characters.

An option would be to transform all capturing groups to alternatives, but that would make the DFAs unnecessarily bigger. It's better to modify the Powerset Construction to take them into account. Let's see an example with a really stupid machine:

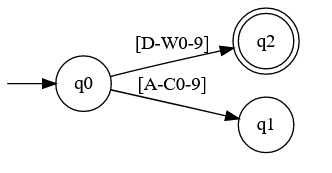
This is a NFA because if it receives a at $q_0$ it could go to both $q_1$ and $q_2$. To transform it to a DFA we'll use the powerset construction but with a difference: We'll split the sets into disjoint subsets.

So the result would be:

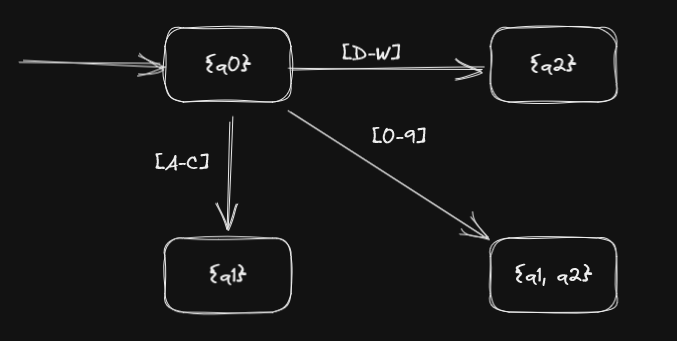
This might be a bit confusing, since I conveniently ignored how the Powerser Construction works in the first place, but... 🥔. The main idea of this section is that you have to adapt it a bit for character classes.

Anchors and multiline mode

Anchors are used to ensure the regex engine is at a certain position. The most used are the start and end of string anchors (^ and $). Both can be more or less replaced in the regex wrapper. Remember that at the beginning of this series all the regex of the engine had an implicit ^, and we fixed it in the post Finding multiple matches. This was because the machine only tries the input starting at a certain position, so if you want to search other positions you have to run the machine multiple times.

So to implement ^, the wrapper could do regexStr[0] === '^', and if it's true it only runs the machine starting in the first position of the string. And the $ could be checked after computing the machine:

compute(string) {
    const memory =  this.nfa.compute(string);
    if (!memory) return null;
    const result = {groups: {}};
    for (const [group, start, end] of Object.values(memory.GROUP_MATCHES)) {
        result.groups[group] = string.substring(start, end);
        if (this._endAnchor && group === 0 && end !== string.length) {}
            return null; // <--- Fail if there's a '$' anchor but the group 0
                          // (which always contains the whole match) is not the same length as the string
    }
    return result;
}

Of course this wouldn't work for bogus regex that can't match, like a^$b. And this also only works for normal mode, not multiline mode. I'm not sure if there is a better way to implement those or any of the other million types of anchors.

A possibility could be doing the same thing as in NFAs. Anchors don't consume input, which makes them kind of epsilon transitions. But as I said two years ago at the beginning of the post, as long as you don't have alternatives like in the image below it might not break anything... probably.

Though I guess that the anchor might not allow full DFA minimization, since it acts as a barrier (a fake character). I haven't found info on the topic.

Finding multiple matches

This would be the same as in the NFA. Finally, something easy.

Atomic groups

Atomic groups are non-capturing groups that, once exited, the engine can't backtrack that decision. But... DFA don't use backtracking, so atomic groups don't make sense in DFAs. We don't have to implement anything!

Backreferences

Breath in... breath out...Breath in... breath out. Okay... let's deal with this fast. To begin with, we need capturing groups for backreferences, so we need to have either a TDFA or a nDFA.

But even with those, the main problem of backreferences is that to implement them in the NFA we made a matcher that is able to consume multiple characters in a single transition. This doesn't cause conflicts because in NFA the machine follows the pattern, but in DFA it would be impossible, it simply can't consume multiple characters in a single transition.

So is it even possible? Maybe? You could do it by repeating the group and then checking if it's actually the same. For example (a|b)\1 would be replaced with (a|b)(a|b), and when the machine ends it would have to check that the value of group 1 is the same as group 2. And of course, it would have to map the group numbers of the original regex to the new regex, since all this should be done in the background without the user noticing.

But I doubt this would work for all cases, specially when the capturing group repeats and its value gets overwritten in the middle of the execution. Maybe the check could be done as soon as it exits the group that replaces the backreference?

This is a complicated problem, and it can be seen in the fact that most DFA or hybrid engines, like Google's re2 or rust's built-in implementation lack backreferences.

The end

Even though DFAs offer huge speed benefits, the complexity involved in implementing modern features makes NFA look a lot better. In the end it's a tradeoff. If you want a really fast engine, you'll miss some features. On the other hand, (extended) NFA can give you incredible recognizing power. The PCRE engine even has recursion and allows defining subpatterns with the syntax (?(DEFINE)...). Alledgely it can even pase context-free languages, which are the level above regular languages in Chomsky's hierarchy.

You might be asking, are there DFA engines in the real world?

Regex implementation are based on two main kind of engine: DFA and NFA. Perl, Java, .NET languages, PHP, Python, Ruby,... and most tools implement a Traditional NFA engines. Some less widespread tools like mawk use a POSIX NFA engine which is a variation of the previous one. Awk, egrep, flex, lex, MySQL,... that mostly needs to verify efficiently the success of an overall match implement the more efficient DFA engine. Finally some tools like GNU awk, GNU egrep and Tcl used the best of both world with an hybrid NFA/DFA engine.

-- https://www.softec.lu/site/RegularExpressions/RegularExpressionEngines

Of course lexers like flex and lex use DFA, since they don't need to implement things like capturig groups. In the future I would like to make my own lexer and I'll probably follow the DFA approach. How do others like mysql implement capturing groups and backreferences? I have no idea.

All I wanted to do is learn how regex worked and to make my own toy regex engine, so for me NFA were a obvious solution. Plus they were really visual and direct, which helps in debugging and in writing a blog series about it.

And with this post, which is just an extremely big ramble, I end my journey with this regex engine. I still could implement more features, but I think the engine already has plenty, and I want to start other projects. Season 2 will probably be implementing a lexer, but that'll have to wait for a while.