- Published on
Implementing a NFA - Building a Regex Engine Part 2
In the introduction we covered how compiling a regex is just building a finite automaton for the language defined by that regex. Now it's time to go deep into what exactly is a finite automaton. First we'll talk about their two types: Deterministic Finite Automata (DFA) and Non-deterministic Finite Automata (NFA). And then we'll implement an NFA and even test it with some simple regex. (YES! Finally we'll write some code 💻)

Finite Automata: NFA and DFA
To talk about NFA and DFA we have to understand what's a Finite Automata. In the last post I already explained it, but just in case, here's a quick refresher. I recommend reading it since it's a more practical explanation plus I also explain how to interpret FA diagrams, and (spoiler alert) you are going to see a lot of those in the following posts. Plus, we all know that you either skipped the introduction or forgot about it.
Optional - What's a finite automata and understanding FA diagrams
An automaton is like a state machine. The machine has certains states connected through transitions.
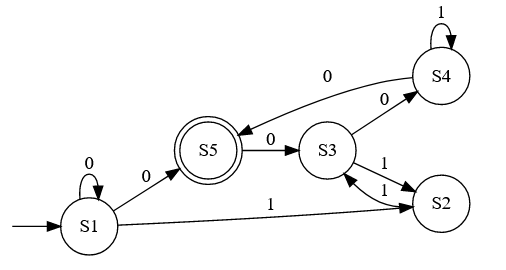
The machine has an starting state, in this example , denoted by an arrow coming from nowhere. The machine starts reading the input one character at a time and moving through transitions. In more advanced machines, like the turing machine, you can decide how to move through the input in each transition. Some might advance the input, others move it backwards or stay in the same position. Finite state machines always read the input from left to right. There is no way to go back. That's why processing an input is usually denoted as consuming it. In the diagram the label of the transition indicates the input character it consumes.
To succeed, some types of machines require to consume all the input AND end in a final state. Others succeed the moment they enter a final state. The machine can have multiple end states. In the example above there is a single ending state, , represented with a double circle.
Since the output is "success" or "error", this type of automaton is also called acceptor. There are other categories of automaton where the machine can have more complex output, for example transducers, which can generate an output string.
Here are some examples of the states the machine above follows given several inputs. Note that some states have two transitions with the same label. I'll talk about this later, since this is one of the differences between DFA and NFA. The machine succeeds if there is at least one path where it succeeds. Therefore it can't fail until it has tested all the possibilities.
| Input | Path | Result |
|---|---|---|
| 0000 | Success | |
| 1111010 | Success | |
| 10 | 😔 | Fail |
| 001 | 😔 | Fail |
Finite automata have a finite number of states (I'm sure you didn't expect that) and don't have memory besides the state they're in.
This means that in order to remember something it needs to have a state that specifically represents that something. In the last post we saw
the example of how you can't build a finite automaton for the language because you have to store the value
n in order to consume the same number of bs than as. For you need 6 () states, 3 with a transitions and 3 with b
transitions. So if n is infinite, it would need an infinite number of states.
Now, let's enter a slightly more formal definition of a finite state machine. DON'T PANIC! Think of it as pseudocode. A machine is formed by:
- A set of states
- A number of transitions, often represented by a function with the form
- A starting state , where is in ( )
- A set of final states . It has to be a subset of ()
The magic is that the properties of the transition function determines if the machine is deterministic or non-deterministic. In a deterministic machine the next state is determined only by the current state and the input received. Wait... Since finite automata don't have memory, what else can determine the next state? What the heck is a non-deterministic automata?
There are situations where a machine doesn't have a obvious state to move to. For example, in the machine below, what happens if the machine
receives the string 0?
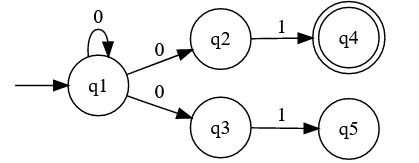
The answer is "it depends". Non-deterministic automata have choices, and which one they pick depends on which transition they prioritize.
An engine that returns a different result in each execution would be useless. That's why the machine always checks all possible paths till
it finds out one that succeeds. For the input 01 the machine could go to or , and since one of them is a final state
it will always accept the string, no matter if first it goes to or if it goes directly to .
Thats the gist of NFA and DFA. But these definitions have some implications:
- Every DFA is a NFA, but not all NFA are DFA
- NFA allow -transitions. These are empty transitions that don't consume any input. The machine can decide whether to move through an epsilon transition or stay where it is.
- If a machine allows three types of input characters (this is formally known as the machine's alphabet) a deterministic machine
has to define the transition for each character IN EVERY STATE 😱.
- That said, most DFA diagrams ignore this assuming the transitions that aren't defined go to a dead state. This is a state where,
once it's entered, it just loops over itself till it consumes the input. Here's an example:
I think we'll keep using the simplified diagram, for obvious reasons.
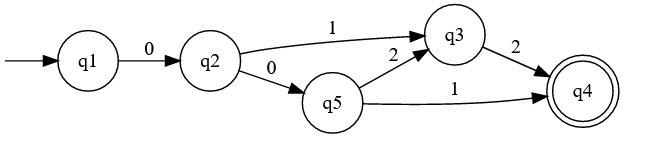 Simplified diagram
Simplified diagram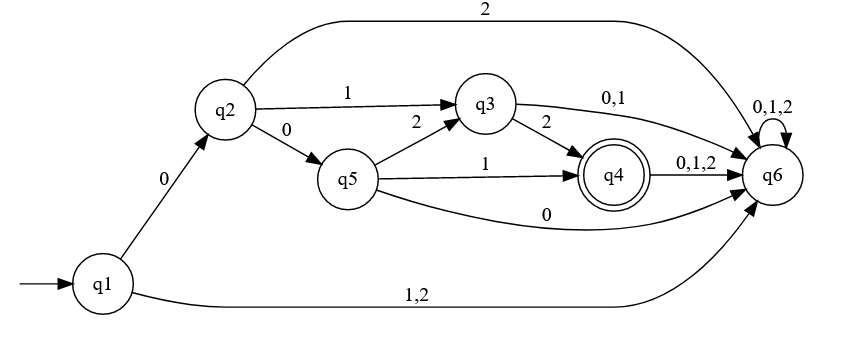 Full diagram with dead state
Full diagram with dead state - In a DFA states can't have two transitions that consume the same input.
- That said, most DFA diagrams ignore this assuming the transitions that aren't defined go to a dead state. This is a state where,
once it's entered, it just loops over itself till it consumes the input. Here's an example:
Enough definitions. How does using a NFA or a DFA affect a regex engine? Both types are equivalent in terms of recognizing power. For every NFA you can find a DFA that recognizes exactly the same language. The main differences is NFA are more intuitive to build, but take more time to execute, since if they make a wrong decision they have to backtrack. On the other hand DFA are faster but might require much more memory. If a NFA has states, the equivalent DFA can have up to states. For more info look up the Powerset construction
I'll talk about why I picked NFA in a latter post. But as a small spoiler, the Powerset Construction is an algorithm for transforming NFA to DFA, but it only applies to pure NFA. In order to implement modern features we'll break some of the concepts of the NFA, so the algorithm can't be used as it is.
Here's an example of a DFA and NFA representing the regex (a|b)*a(a|b). I purposely picked a regex where the DFA is way less
intuitive than the NFA. Of course that's not always the case, but for most non-trivial regex it is.
The NFA was built using Thompson construction, a method I'll explain in the next post, and it leads to a machine that is clearly divided
into pieces
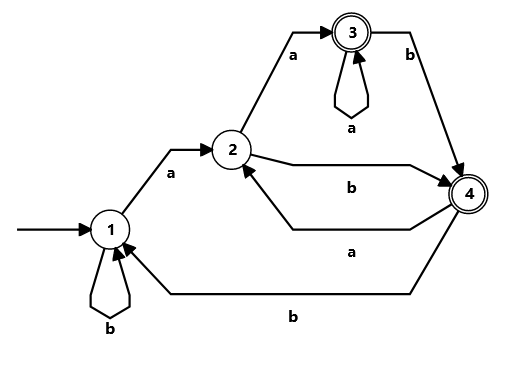
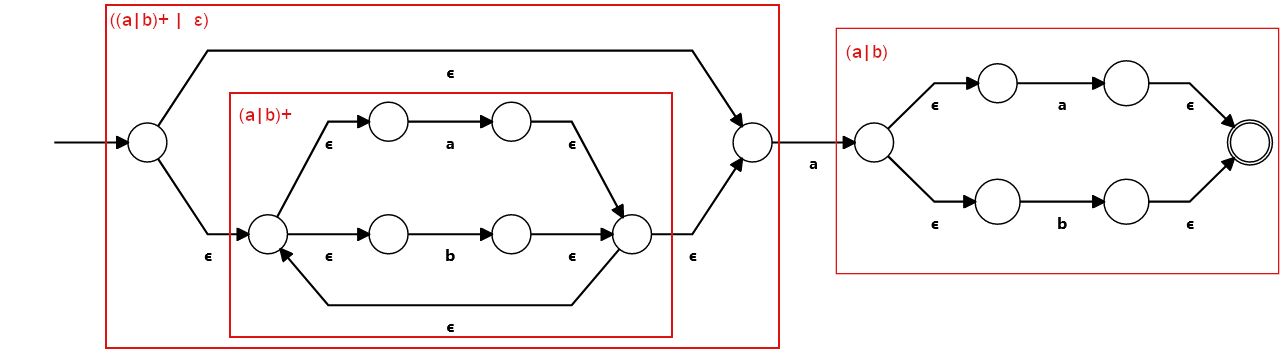
Note that the DFA is minimized (it has the least number of states possible) while the NFA has a lot of unnecessary states. It would have been easy for me to optimize the NFA by hand, but I wanted to show the same one that will be generated by our engine. There are efficient minimization algorithms for DFA, but sadly, for NFA it's NP-hard 😞.
And that's all we need to know about finite automata. Let's get into some code!. But first, since this is a post about finite automata the law forces me to make a meme about the videogame Nier Automata so here it is:

NFA implementation
I'll do this in Javascript because it's how I made the web app. We won't be using any libraries, so feel free to use whatever language you prefer. Also for the sake of simplicity I'll ignore some error management checks.
I'm going to focus on making the NFA more readable rather than optimize every single bit. For that reason, the API will use string names and internally it'll be translated its specific state object. When we finish this section we'll be able to run something like this:
const nfa = new EngineNFA();
nfa.declareStates("q0", "q1");
nfa.setInitialState("q0");
nfa.setEndingStates(["q1"]);
nfa.addTransition("q0", "q1", new CharacterMatcher("a"));
console.log(nfa.compute("a"));
Defining the structure
State and transitions
A state is a set of transitions, and a transition is just a matcher and the state where the transition goes.
class State {
constructor(name) {
this.name = name;
this.transitions = [];
this.startsGroups = [];
this.endsGroups = [];
}
addTransition(toState, matcher) {
this.transitions.push([matcher, toState]);
}
unshiftTransition(toState, matcher) {
this.transitions.unshift([matcher, toState]);
}
}
You might wonder why I implemented the unshiftTransition. NFA need to define a way of choosing a path when there are multiple
options. Our machine will prioritize transitions in the same order they are in this.transitions. So unshiftTransition
means "add this transition and give it the highest priority".
Matchers
If we were to implement just formal regex, a matcher could be as simple as a single letter. The matcher "a" would match the
character a, and the matcher null would represent an epsilon transition. For this post, that would be enough, but in the following
ones we'll expand it to implement character classes like [a-zA-Z0-9], anchors and more. So as a teaser let's implement a simple interface:
class Matcher {
// Returns true if 'char' can be consumed by the matcher
matches(char) {
return false;
}
// We need to know when it's an epsilon transition to avoid consuming input
isEpsilon() {
return null;
}
get label() {
return "undefined-matcher"
}
}
class CharacterMatcher extends Matcher{
constructor(c) {
super();
this.c = c;
}
matches(char) {
return this.c === char;
}
isEpsilon() {
return false;
}
get label() {
return this.c;
}
}
class EpsilonMatcher extends Matcher {
// An epsilon matcher always matches
matches() {
return true;
}
isEpsilon() {
return true;
}
get label() {
return "ε";
}
}
The label is for debugging, and will be more useful when we define more types of matchers.
The machine
The interface of the machine uses strings to make it more readable, but if you want to make the most efficient NFA ever you can just use references to the state object.
class EngineNFA {
constructor() {
this.states = {};
this.initialState = null;
this.endingStates = null;
}
setInitialState(state) {
this.initialState = state;
}
setEndingStates(states) {
this.endingStates = states;
}
addState(name) {
this.states[name] = new State(name);
}
declareStates(...names) {
for (const n of names) this.addState(n);
}
addTransition(fromState, toState, matcher) {
this.states[fromState].addTransition(this.states[toState], matcher);
}
/**
* Like 'addTransition' but the transition is given the highest priority
*/
unshiftTransition(fromState, toState, matcher) {
this.states[fromState].unshiftTransition(this.states[toState], matcher);
}
compute(string) {
// We'll see this on the next section
}
}
Executing the machine

Now we have the structure of an NFA defined, but we need to execute it. There are two main ways of doing it:
- Non-backtracking implementation: A NFA machine can be considered as being at multiple states at the same time.
- Backtracking implementation: The machine follows a single path and if it fails it backtracks to the last decision it made.
I'm not completely sure of the consequences of each implementation. The backtracking implementation suffers from catastrophic backtracking, but I guess that the regex that provoke it need an insane amount of memory in non-backtracking implementations. Still, this is just a guess and I would rather not enter this topic here. Maybe I'll investigate it and make a future post.
For the sake of simplicity I'll implement an iterative backtracking implementation.
Optional - More about the non-backtracking implementation
A NFA could be seen as a machine that is at several states at the same time. For a formal regex engine you could store a set of current states and in each iteration compute the input for each state. If a state doesn't have a transition for that input, it's removed, and if it has multiple transitions all the next states are added to the set.
This only works because the machine doesn't care how you got to a state. The only thing that matters is the current state and the current input. This get's a bit more complicated when we add capturing groups, since the machine captures a different text depending on the path taken.
A way to do this is to consider each choice as the machine branching into two submachines. Each one has a copy of the memory of the parent machine, and all the submachines work in parallel. This might sound crazy, but it's how antlr4 works.
The idea behind the ALL(*) prediction mechanism is to launch subparsers at a decision point, one per alternative production. The subparsers operate in pseudo-parallel to explore all possible paths. Subparsers die off as their paths fail to match the remaining input. The subparsers advance through the input in lockstep so analysis can identify a sole survivor at the minimum lookahead depth that uniquely predicts a production.
This is just an example since antlr4 isn't a finite automata, though since it's a context-free parser I guess it's like a pushdown automata, at least at the basic level. Antlr4 allows to write code in actions and predicates, so it allows some context-sensitive grammars.
I'll make an iterative implementation rather than a recursive one because this way I have more control over the stack. This can be useful to implement atomic groups, which are capturing groups that delete the stack after they are consumed. That said, currently my engine doesn't have atomic groups, but I'll consider implementing them.
Optional - What are atomic groups
An atomic groups is a group where, once you exit it, the engine can't backtrack that decision. Therefore, the regex will fail in cases where it wouldn't without atomic groups.
As a simple example, the regex a(?>bc|b)c matches
abcc but doesn't match abc. If you replace the atomic group with a regular group, it matches.
In the second case the engine matches the bc with the
first alternative of the group, it exits it and expects a c, so it fails. But since it's an atomic group, it can't backtrack
and it just rejects the string. You can find more info about atomic groups
in https://www.regular-expressions.info/atomic.html (which is where I extracted the example)
This topic is important in an engine implementation because it makes the engine much more sensitive to the way it prioritizes choices,
since if it makes the wrong one, it can't go back. Following the previous example, if you swap the position of the alternatives
(a(?>b|bc)c) now it matches abc. That's becauses the engine where I tested this (PCRE in https://regexr.com/) prioritizes the alternatives in the
order they are written.
The programmer is responsible for making the regex he wants right, but the engine should state clearly how it prioritizes so the programmer can make the right decisions.
We'll change this method in the future to add capturing groups. For now let's make a simple implementation that returns true or false.
compute(string) {
const stack = [];
// Push the initial state to the stack
// - The i is the current position in the string
stack.push({i: 0, currentState: this.states[this.initialState]});
while (stack.length) {
const {currentState, i} = stack.pop();
if (this.endingStates.includes(currentState.name)) {
return true;
}
const input = string[i];
// Transitions are pushed in reverse order because we want the first transition
// to be in the last position of the stack. Stacks are LIFO (Last In, First Out)
for (let c = currentState.transitions.length-1; c >= 0; c--) {
const [matcher, toState] = currentState.transitions[c];
if (matcher.matches(input, i)) {
// Reminder: Epsilon transitions don't consume input
const nextI = matcher.isEpsilon() ? i : i+1;
stack.push({i: nextI, currentState: toState});
}
}
}
return false;
}
Optional - Another possible implementation
This is an optional section for the people that have inmediately thought: "But can't you implement it this other way?". The answer is YES. In fact, the regex engine I made for the github project has two iterative algorithms. The first is the one above (improved with modern features) and the other one is what I called the "animation" algorithm, since it generates smoother animations.
The main difference is that the "animation" algorithm only pushes the first matching transition of a state, and only removes that state from the stack when it has checked all its transitions. For that it needs to remember which transitions has already covered.
The implementation I made in the project was a bit lazy and instead pops the element and repushes it with a different index. The animation page in my project was a last-minute addition and I was tired of programming the engine. Here's the lazy implementation, but it would be much cleaner and intuitive if it did what I said in the previous paragraph.
const current = stack.pop();
const {currentState, i, nextTransition} = current;
// ...
for (let c = nextTransition; c < currentState.transitions.length; c++) {
const [matcher, toState] = currentState.transitions[c];
if (matcher.matches(input, i)) {
const nextI = matcher.isEpsilon() ? i : i+1;
stack.push({...current, nextTransition: c + 1}) // To backtrack if it fails
stack.push({nextTransition:0, i: nextI, currentState: toState});
break; // <-- Important: Add only one transition to the stack
}
}
return false;
I called this the "animation" version because it produces a smoother animation when the engine backtracks. Instead of moving to another transition that was added to the stack in a choice that happened 5 minutes ago, it literally goes back to the previous state. This is also more debuggable, but I decided to focus on the other implementation in this posts since it's more direct.
Now that we have all the ingredients, let's test it. This is a (weird) NFA for the regex ab+:
const nfa = new EngineNFA();
nfa.declareStates("q0", "q1", "q2", "q3");
nfa.setInitialState("q0");
nfa.setEndingStates(["q3"]);
nfa.addTransition("q0", "q1", new CharacterMatcher("a"));
nfa.addTransition("q1", "q2", new CharacterMatcher("b"));
nfa.addTransition("q2", "q2", new CharacterMatcher("b"));
nfa.addTransition("q2", "q3", new EpsilonMatcher());
console.log(nfa.compute("abbbbbb")); // True
console.log(nfa.compute("aabbbbbb")); // False
console.log(nfa.compute("ab")); // True
console.log(nfa.compute("a")); // False
The epsilon transition and the q3 state are unnecessary. It's just to test that epsilon transitions work. It seems to work, but there's
a problem, the machine returns true for strings that partially match that input. For example:
console.log(nfa.compute("abc")); // True
This is clearly wrong and easily fixed by adding a condition in the return statement, BUT since we are implementing a modern regex engine, we
don't really want that. Modern regex allow this unless you specify the end of string anchor $. For example in Javascript:
const regex = new RegExp("ab+");
console.log(regex.exec("abbc")); //Array [ "abb" ]
So it's not a bug, it's a feature. When we implement capturing groups it'll be more clear how much text the engine has actually matched.
Epsilon loops
You thought it was over, didn't you? There's a final problem: Epsilon loops.
NFA don't stop till they either consume all the input or reach a final state. But since epsilon transitions don't consume input, if the NFA has epsilon loops it might get stuck forever. Depending on the regex syntax you allow, this might not be a problem. But if you allow empty alternatives or an empty string (usually represented with the epsilon symbol) you have to fix it.
This is the NFA that my engine generates for (|a)*:
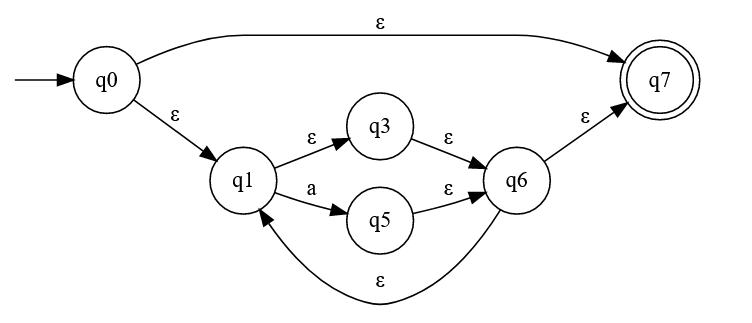
If the machine prioritizes the wrong choices, it might get stuck in an eternal loop: .
First let's see this situation specifically in our machine. It's pretty easy to force it:
const nfa = new EngineNFA();
nfa.declareStates("q0", "q1", "q2");
nfa.setInitialState("q0");
nfa.setEndingStates(["q2"]);
nfa.addTransition("q0", "q1", new CharacterMatcher("a"));
nfa.addTransition("q1", "q1", new EpsilonMatcher());
nfa.addTransition("q1", "q2", new CharacterMatcher("b"));
console.log(nfa.compute("ab")); // Stuck forever :(
Even though there is a transition from to , the engine always prioritizes the first transition, and since it doesn't consume input, it can transverse it infinitely.
To solve this we'll take advantage of the fact that transversing an epsilon loop is useless. The machine can't differenciate between a state that has gone through no epsilon loops and the same state that has gone through a thousand loops. This will still be true when we implement capturing groups, because epsilon transitions don't consume input and therefore don't add characters to the groups.
Taking this into account, we can make the machine remember the states it has entered through an epsilon transition and block it from entering the same state twice Of course after we enter a non-epsilon transition we need to empty this memory.
But... didn't you say finite machines don't have memory? We'll, TeChNiCaLLy this wouldn't be considered part of the machine's memory, instead it's more
like an implementation detail. Plus, when we implement capturing groups we'll need a memory (and in the process, we'll break the
definition of pure NFA), so why wait?
compute(string) {
const stack = [];
// Push the initial state to the stack
// - The i is the current position in the string
stack.push({i: 0,
currentState: this.states[this.initialState],
memory: {EPSILON_VISITED: []} // <-- This is new
});
while (stack.length) {
const {currentState, i, memory} = stack.pop();
if (this.endingStates.includes(currentState.name))
return true;
const input = string[i];
// Transitions are pushed in reverse order because we want the first transition
// to be in the last position of the stack. Stacks are LIFO (Last In, First Out)
for (let c = currentState.transitions.length-1; c >= 0; c--) {
const [matcher, toState] = currentState.transitions[c];
if (matcher.matches(input, i)) {
// The memory has to be immutable. This is the simplest way to make a deep copy of
// an object with only primitive values
const copyMemory = JSON.parse(JSON.stringify(memory));
if (matcher.isEpsilon()) {
// Don't follow the transition. We already have been in that state
if (memory.EPSILON_VISITED.includes(toState.name))
continue;
// Remember that you made this transition
copyMemory.EPSILON_VISITED.push(currentState.name);
} else {
// We are transversing a non-epsilon transition, so reset the visited counter
copyMemory.EPSILON_VISITED = [];
}
// Reminder: Epsilon transitions don't consume input
const nextI = matcher.isEpsilon() ? i : i+1;
stack.push({i: nextI, currentState: toState, memory: copyMemory});
}
}
}
return false;
}
If we run the previous example with this algorithm, it works 😎. Crisis avoided.
Conclusion
We've already seen several examples of NFAs that represent regexes in the last two posts. In the next one we'll focus on an algorithm to translate a regex string to a NFA. With that, we'll already have an engine for formal regex! But that's not enough, we'll also add a lot modern features and make a 💯 regex engine.
Season 1 - Building a Regex Engine (Completed)
- Introduction
- Implementing a NFA
- Creating a NFA from a regex
- Modern features - Part 1: Capturing groups
- Modern features - Part 2: Character classes and escape characters
- Modern features - Part 3: Anchors and multiline mode
- Finding multiple matches
- Modern features - Part 4: Atomic groups
- Modern features - Part 5: Backreferences
- NFA vs DFA